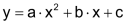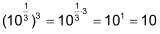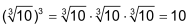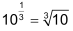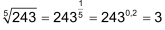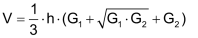Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
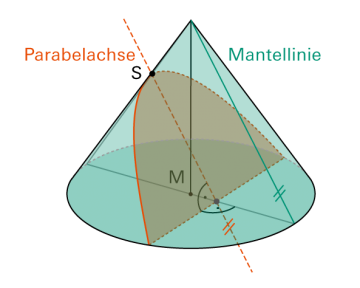
Parabel
 |
|
Schneidet man einen Kegel mit einer Ebene, die parallel zu einer Mantellinie verläuft, so ergibt sich als Schnittkurve eine «Parabel». |
|
Stellt man diese Kurve im Koordinatensystem so dar, dass die y-Achse parallel zur Symmetrieachse der Parabel verläuft, kann man die Kurve mit einer quadratischen Funktionsgleichung beschreiben: |
| Umgekehrt ist der Graph einer solchen Funktion eine Parabel. |
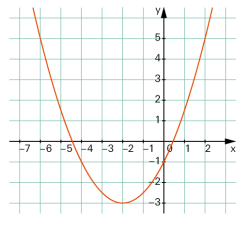 |
| siehe quadratische Funktion |
parallel
Parallelogramm
|
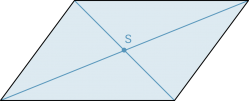
Das Parallelogramm (auch «Rhomboid») ist ein Viereck, bei dem die gegenüberliegenden Seiten parallel sind. |
 |
|
Beachte: |
| Jedes punktsymmetrische Viereck ist ein Parallelogramm, und umgekehrt ist jedes Parallelogramm ein punktsymmetrisches Viereck. |
 |
|
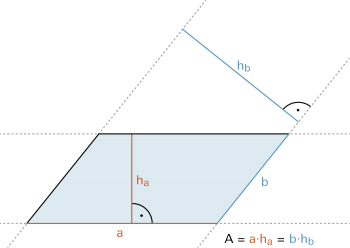
Fläche = Seitenlänge mal zugehörige Höhe (Höhe = Streifenbreite) |
Parameter
| siehe Formvariable |
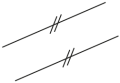
parkettieren
|
Zum «Parkettieren» eignen sich (wenn man nur eine einzige Sorte Vielecke einsetzen will) das Quadrat, das Rechteck, das Parallelogramm und damit auch jedes Dreieck – aber auch ein allgemeines Viereck, ein reguläres Sechseck und diverse weitere Vielecke mit speziell abgestimmten Längen und Winkeln. |
|
Siehe auch reguläres Parkett, Penrose-Parkett |
Penrose-Parkett
|
Nichtperiodische Parkette mit einer kleinen Anzahl verschiedener Bausteine, mit denen sich zwar parkettieren lässt, sich aber kein regelmässig wiederholendes Muster einstellt. Der Mathematiker Roger Penrose (* 1931) hat als einer der Ersten solche Parkette gefunden.
|
Peripheriewinkel
| Siehe Kreiswinkelsätze |
Permutation
| «Permutation» ist ein Begriff aus der Kombinatorik. Als Permutation bezeichnet man allgemein eine Um- oder Anordnung von Elementen einer Menge. |
|
Beispiel |
| Oft spricht man auch von «Permutationen einer Menge» und meint damit einzig die Anzahl der möglichen Anordnung ihrer Elemente. |
| Beispiel Bei fünf Elementen a, b, c, d und e gibt es 120 (= 5 · 4 · 3 · 2 · 1) Möglichkeiten, bei den erwähnten drei Ziffern gibt es 6 (= 3 · 2 · 1) Möglichkeiten unterschiedlicher Anordnung. |
| siehe auch Fakultät |
platonische Körper
|
Ein «platonischer Körper» ist ein regelmässiges Polyeder: Alle Begrenzungsflächen sind zueinander kongruente regelmässige Vielecke, und an jedem «Knoten» treffen gleich viele Vielecke aufeinander. |
|||
 |
|||
| Es gibt nur fünf platonische Körper. Grund: Alle Winkel an einem Knoten müssen zusammen weniger als 360° gross sein, und es müssen dort mindestens drei Flächen aufeinander treffen. Das kann nur erfüllt werden durch |
|||
| ♦ ♦ ♦ |
3 regelmässige Fünfecke 3 Quadrate 3, 4 oder 5 gleichseitige Dreiecke |
→ → → |
Dodekaeder Würfel Tetraeder, Oktaeder und Ikosaeder |
|
Jeder platonische Körper besitzt eine In- und eine Umkugel mit gemeinsamem Zentrum. |
|||
platonisches Parkett
| Siehe reguläres Parkett |
Polyeder
|
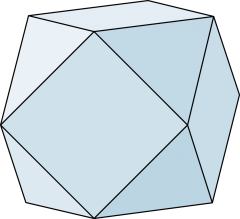
Aus dem Griechischen («Vielflächer») stammende Bezeichnung für einen Körper, der durch (ebene) Vielecke begrenzt wird. |
|
 |
|
|
Der abgebildete Kuboktaeder zum Beispiel kann durch gleichmässiges Abschleifen der Ecken eines Würfels je bis in die Kantenmitten erzeugt werden. Er besteht aus 6 Quadraten und 8 gleichseitigen Dreiecken, hat 12 Ecken und 24 Kanten. |
|
|
Wichtige spezielle Formen |
|
| ♦
♦ |
reguläre Polyeder (siehe platonische Körper) |
Polygon
| Bezeichnung aus dem Griechischen für Vieleck. |
| siehe auch Innenwinkel |
Potenz [ zurück ]
| Ein Produkt aus mehreren gleichen Faktoren kann man als Potenz schreiben. |
|
3 • 3 • 3 • 3 • 3 = 35 |
 |
|
Für grosse (und auch für sehr kleine positive Zahlen) werden Zehnerpotenzen eingesetzt: Basis der Potenz ist dann die Zahl 10. siehe auch Potenzgesetze |
Potenzgesetze
|
Für Potenzen mit natürlichen Zahlen als Exponenten gelten folgende Gesetze (a bezeichnet die Basis, n und k die Exponenten): |
||
| Gesetz 1 | 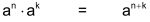 |
|
| Gesetz 2 | 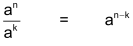 |
|
| Gesetz 3 | 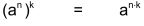 |
|
|
Bei Potenzen mit positiven Basen sind die Zahlen 0 und 1 sowie negative Zahlen als Exponenten sinnvoll. Dies lässt sich mit dem Gesetz 2 zeigen: |
||
 |
||
| Auch Brüche als Exponenten sind bei Potenzen mit positiven Basen sinnvoll. | ||
|
Laut Gesetz 3 gilt:
|
||
|
Aus der Definition der Wurzel folgt:
|
||
|
Weil das Ergebnis beider Gleichungen (im Beispiel = 10) identisch ist, gilt somit
(Vergleiche die Ausdrücke in den Klammern der beiden identischen Gleichungen.) |
||
|
Mit Taschenrechnern, welche eine «yx»-Taste haben, lassen sich so Wurzeln direkt berechnen. |
||
|
Beispiel
|
||
Primfaktorzerlegung
| Natürliche Zahlen, die nicht Primzahlen sind, lassen sich oft auf mehrere Arten in ein Produkt zerlegen. Die auftretenden Faktoren heissen Teiler. | |
| Wenn man als Faktoren nur Primzahlen wählt, heisst die Zerlegung «Primfaktorzerlegung». Die Primfaktorzerlegung ist eindeutig. | |
|
Beispiele: |
|
|
30 = 2 · 3 · 5 90 = 2 · 32 · 5 68'607 = 34 · 7 · 112 |
|
Primzahl
|
Bei den natürlichen Zahlen unterscheidet man die «Primzahlen» von den «zusammengesetzte Zahlen». |
||||||||||||||||||||||||||
|
Primzahlen lassen sich nur durch 1 und sich selbst teilen. Eine Primzahl hat demnach genau zwei (unechte) Teiler: die Zahl 1 und sich selbst. Die Zahl 1 ist nach diesen Kriterien keine Primzahl (sie hat nur einen Teiler). |
||||||||||||||||||||||||||
|
Es gibt unendlich viele Primzahlen. |
||||||||||||||||||||||||||
|
Zusammengesetzte Zahlen lassen sich in eindeutiger Weise in Primfaktoren zerlegen, aus denen sich alle Teiler der betreffenden Zahl gewinnen lassen. |
||||||||||||||||||||||||||
|
Beispiel: |
||||||||||||||||||||||||||
|
60 = 2 · 30 = 2 · 2 · 15 = 2 · 2 · 3 · 5 |
||||||||||||||||||||||||||
|
Folgende Zahlen sind echte Teiler von 60: 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 |
||||||||||||||||||||||||||
|
Primzahlen zwischen 1 und 100 |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
Primzahlen spielen beim Verschlüsseln von Dokumenten (Kreditkarten, Mailverkehr) eine zentrale Rolle. |
||||||||||||||||||||||||||
Primzahlzwillinge
|
Ausser bei den Zahlen 2 und 3 sind zwei Primzahlen immer mindestens zwei Schritte auf dem Zahlenstahl voneinander entfernt. Zwei Primzahlen, die sich um genau 2 unterscheiden, heissen «Primzahlzwillinge». |
|
|
Beispiele: |
|
|
(3;5), (5;7), (11;13), (17;19) aber auch (71;73) oder (1'019;1'021) |
|
|
Primzahlzwillinge werden «gegen oben» immer seltener. Stark zu vermuten ist, dass es trotzdem unendlich viele Primzahlzwillinge gibt. Erstaunlicherweise konnte dies aber bis heute nicht bewiesen werden. |
|
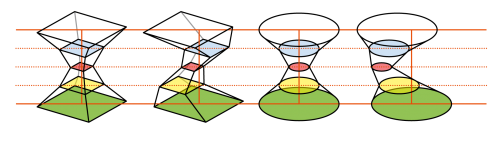
Prinzip von Cavalieri
|
Der italienische Mathematiker Bonaventura Cavalieri (etwa 1598-1647) hat das folgende Prinzip formuliert: |
|
Mit dem Prinzip von Cavalieri lassen sich zum Beispiel das Volumen eines schiefen Prismas, eines schiefen Zylinders oder auch das Kugelvolumen ermitteln. |
 |
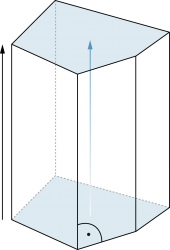
Prisma
|
Verschiebt man ein Vieleck senkrecht zur Ausgangslage durch den Raum, so überstreicht es ein (gerades) Prisma. Grund- und Deckfläche sind kongruent, die Seitenflächen sind Rechtecke. |
 |
|
Quader und Würfel sind spezielle gerade Prismen. |
|
Erfolgt die Verschiebung des Vielecks nicht senkrecht («schräg») zur Ausgangslage, so spricht man von einem «schiefen Prisma». |
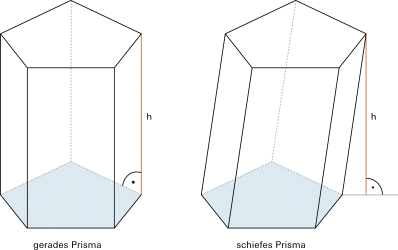 |
Produkt
| Siehe Multiplikation |
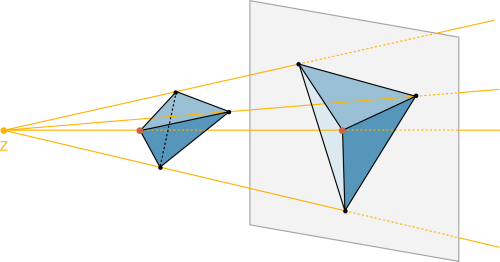
Projektionen
|
Um räumliche Objekte auf einem Blatt Papier darzustellen, gibt es verschiedene Möglichkeiten: |
|
Zentralprojektion |
|
Parallelprojektion |
|
Fallen die Lichtstrahlen senkrecht auf die Bildebene, so spricht man von einer «senkrechten Projektion» oder «Normalprojektion». Fallen die Lichtstrahlen hingegen in einem andern Winkel auf redet man von einem Schrägbild. |
| Oft ist es vorteilhaft, von einem Objekt mehrere Normalbilder herzustellen, z.B. von oben, von vorne und von der Seite. Man spricht dann von «zugeordneter Normalprojektion». |
| siehe Risse |
Promille
|
Promille (‰) bedeutet «Tausendstel» (lateinisch PRO MILLE «von tausend»). |
|
Beispiel: |
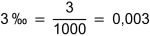 |
|
Promillegrenze: |
proportional
|
Zwei Grössen x und y heissen «proportional» zueinander, wenn das Verdoppeln (Halbieren, Dritteln, …) der einen Grösse das Verdoppeln (Halbieren, Dritteln, …) der anderen Grösse bewirkt. |
| Stellt man die proportionale Abhängigkeit zweier Grössen in einem Koordinatensystem dar, ergibt sich eine Gerade durch den Ursprung. |
|
In der Wertetabelle erkennt man Proportionalität daran, dass der Quotient aus zugeordneten Werten konstant ist, ausgenommen das Paar (0/0). |
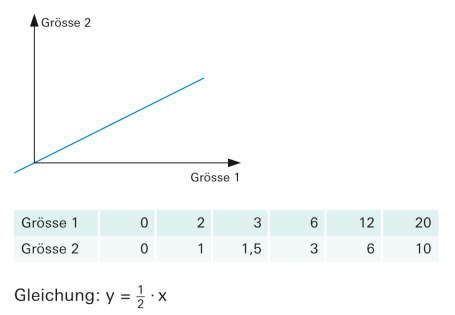 |
|
Die konstante Grösse k in der Gleichung y = k · x heisst «Proportionalitätsfaktor» oder «Proportionalitätskonstante». |
| Siehe auch umgekehrt proportional |
Prozent
|
Prozent (%) bedeutet «Hundertstel» (lateinisch PRO CENTUM «von hundert»). |
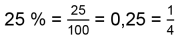 |
Punkt vor Strich
|
Diese Abmachung legt fest, dass beim Rechnen Mal- und Divisionszeichen («Punktoperationen», «Operationen zweiter Stufe») stärker binden als Plus- und Minuszeichen («Strichoperationen», «Operationen erster Stufe»). |
| Siehe Rechengesetze |
Punktoperation
|
Multiplikation und Division heissen «Punktoperationen», weil ihre Operationszeichen aus Punkten bestehen (Operationen zweiter Stufe). |
|
Siehe auch Punkt vor Strich |
Punktspiegelung
|
Die Punktspiegelung ist eine spezielle Kongruenzabbildung: Sie entspricht der Drehung einer Figur in der Ebene um einen Winkel von 180°. |
||
|
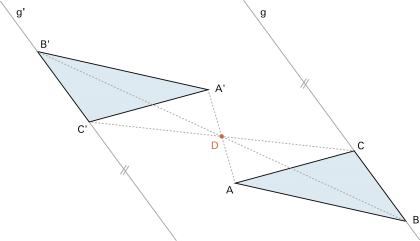
Konstruktiv ist sie – einfacher als durch einen Drehvorgang – wie folgt auszuführen: Das Bild P' eines Punktes P erhält man, indem auf einem Strahl von P durch den Drehpunkt D der Abstand auf die andere Seite abgetragen wird (der Drehpunkt D ist dann Mitte von ). ). |
||
|
Beispiel: |
Punktspiegelung eines Dreieckes ABC. | |
|
|
 |
|
| Beachte: | Original und Bild einer Geraden sind jeweils parallel. | |
|
Punktsymmetrische Figuren |
||
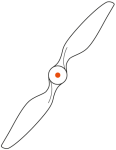
| Gibt es bei einer Figur einen Drehpunkt D so, dass nach einer Drehung um 180° die Figur exakt gleich aussieht wie vorher, heisst sie «punktsymmetrisch». Den Drehpunkt D nennt man in diesem Fall auch «Symmetriezentrum». | ||
|
Propeller und viele Spielkarten sind punktsymmetrische Figuren. |
||
  |
||
|
Beachte: |
Jedes Parallelogramm ist ein punktsymmetrisches Viereck. | |
Punktsymmetrie
| Siehe Punktspiegelung |
Pyramide
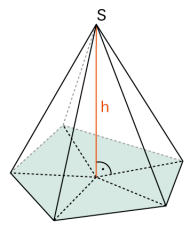
| Pyramiden sind Körper mit einem n-Eck als Grundfläche und n Dreiecken mit gemeinsamer Spitze S als Mantelfläche. Höhe h ist der Abstand von S zur Grundfläche. | |
 |
|
| Spezialfälle | |
| ♦ | einer «dreiseitigen Pyramide», d.h. man zählt die Standfläche nicht mit.) |
| ♦ | Regelmässige Pyramide: Die Grundfläche ist ein reguläres n-Eck, alle Kanten, die in S zusammenlaufen, sind gleich lang, damit liegt die Spitze S senkrecht über dem Mittelpunkt der Grundfläche. |
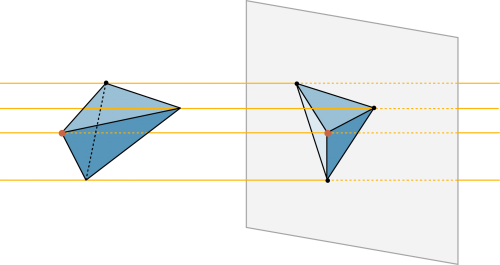
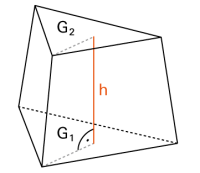
Pyramidenstumpf
 |
|
Mit G1 und G2 als Boden- und Deckelfläche ergibt sich das Volumen: |
Pythagoras-Satz
| Siehe Satz des Pythagoras |