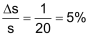Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
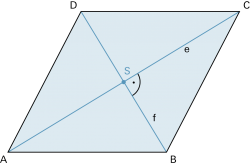
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
radioaktiver Zerfall
|
Viele Isotope eines Elements sind instabil: |
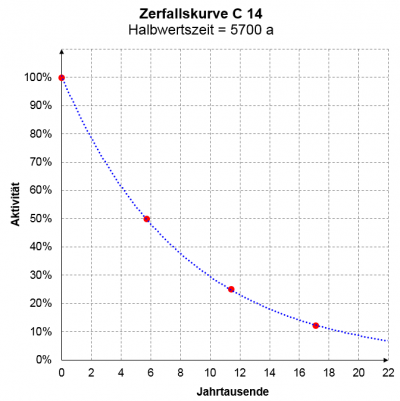 |
rationale Zahlen
Alle Zahlen, die sich als Bruch in der Form 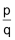 darstellen lassen, heissen rationale Zahlen (p und q sind ganzzahlig mit q ≠ 0). Abgekürzt wird diese Menge mit dem Symbol darstellen lassen, heissen rationale Zahlen (p und q sind ganzzahlig mit q ≠ 0). Abgekürzt wird diese Menge mit dem Symbol 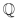 . Auch die ganzen Zahlen gehören zu dieser Menge. . Auch die ganzen Zahlen gehören zu dieser Menge. |
||
| Statt als Bruch kann eine rationale Zahl im Zehnersystem auch als abbrechender oder periodischer Dezimalbruch geschrieben werden: | ||
| • | ganz oder abbrechend: | 4 3,5 0,875 |
| • | periodisch: | 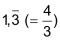 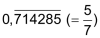 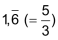 |
| Dezimalbrüche, die nach dem Komma und vor der Periode eine oder mehrere Ziffern aufweisen, werden oft «gemischt-periodisch» genannt: | ||
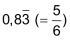 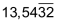 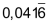 |
||
| Mit den rationalen Zahlen kann man uneingeschränkt addieren, subtrahieren und multiplizieren. Man kann auch uneingeschränkt dividieren, ausser durch 0. Das Ergebnis einer solchen Operation ist immer wieder eine rationale Zahl. | ||
 |
||
Nicht in den Bereich der rationalen Zahlen fallen Zahlen wie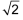 oder π, die sich in Dezimalbruchdarstellung weder als abbrechend noch als periodisch (oder gemischt periodisch) erweisen – und sich damit auch nicht als Bruch darstellen lassen. oder π, die sich in Dezimalbruchdarstellung weder als abbrechend noch als periodisch (oder gemischt periodisch) erweisen – und sich damit auch nicht als Bruch darstellen lassen. |
||
| Siehe auch irrationale Zahlen | ||
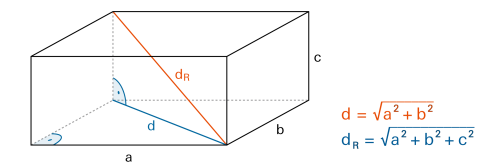
Raumdiagonale im Quader
|
Durch zweimaliges Anwenden des Satzes von Pythagoras ergibt sich die Länge der Quader-Raumdiagonalen (dR). |
 |
|
Die Raumdiagonale eines Würfels mit Kantenlänge a beträgt: |
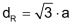 |
Rechengesetze
| Kommutativgesetz | a + b = b + a a · b = b · a |
|
|
|
|
Assoziativgesetz |
a + (b + c) = (a + b) + c a · (b · c) = (a · b) · c |
|
Distributivgesetz |
a · (b + c) = (a · b) + (a · c)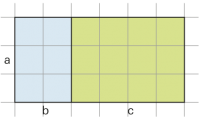 |
|
Zudem ist die Regel «Punkt vor Strich» zu beachten. |
|
|
|
|
|
Klammerregel 1 |
10 – (2 + 5) = 10 – 7 = 3 |
| Operationen in den Klammern rechnet man zuerst. | |
| Klammerregel 2 | 2 · (8 – (1 + 4)) = 2 · (8 – 5) = 2 · 3 = 6 |
| Bei ineinander geschachtelten Klammern rechnet man von innen nach aussen. | |
| Regel 3 | 7 · 8 : 4 = 56 : 4 = 14 |
| Rechnungen mit mehreren Punktoperationen rechnet man von links nach rechts. Beachte aber: | |
| 7 · (8 : 4) = 7 · 2 = 14 | |
| Regel 4 | 13 – 2 · 4 = 13 – 8 = 5 |
| Punktoperationen binden stärker als Strichoperationen. Beachte: |
|
| (a + b) · c ≠ a + b · c («Punkt vor Strich») | |
| Siehe auch Bruchoperationen | |
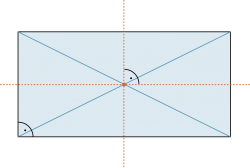
Rechteck
 |
|
|
Das Rechteck ist ein Viereck mit lauter rechten Winkeln. |
|
|
Weitere Eigenschaften des Rechteckes: |
|
|
• |
Die Diagonalen sind gleich lang. |
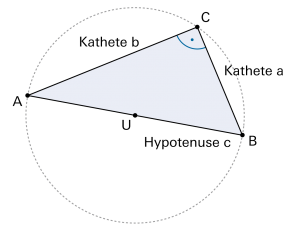
rechtwinkliges Dreieck
|
Das rechtwinklige Dreieck spielt in der Mathematik eine derart zentrale Rolle, dass seine Teile eigene Namen haben: |
 |
|
Für das rechtwinklige Dreieck gilt der Satz des Pythagoras: |
|
a2 + b2 = c2 |
reelle Zahlen
| Siehe irrationale Zahlen |
Regelmässiges n-Eck
|
Ein regelmässiges n-Eck ist eine ebene Figur mit n Ecken, bei der alle Seiten gleich lang und alle Innenwinkel gleich gross sind. |
|
|
Ein regelmässiges n-Eck hat sowohl einen Inkreis als auch einen Umkreis. |
|
|
Beispiele: |
|
|
gleichseitiges Dreieck, Quadrat, |
|
|
Der Innenwinkel im regelmässigen n-Eck beträgt: |
|
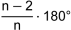 |
|
regulär
| Ausdruck für «regelmässig» |
| Siehe regelmässiges n-Eck |
reguläres Parkett
|
Ein Parkett heisst regulär, wenn ... |
|
|
1. |
alle Stücke regelmässige Vielecke (Polygone) sind, |
|
Wird nur eine einzige Sorte kongruenter regelmässiger Vielecke eingesetzt, heisst das Parkett platonisch. Offenbar gibt es bloss drei Möglichkeiten dazu: |
|
|
Wenn zwei oder mehr Sorten regulärer Vielecke eingesetzt werden, heisst das Parkett archimedisch. |
|
 |
|
| platonisch archimedisch weder-noch | |
| Siehe auch Vieleck, regelmässiges | |
relative Häufigkeit
| Siehe Häufigkeit |
relativer Fehler
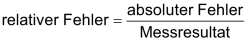 |
|
| Eine Messungenauigkeit von Δs = ±1 cm ist bei einer Länge von s = 20 cm natürlich viel einschneidender, als wenn die Länge s = 20 m beträgt. | |
|
♦ |
Relativer Fehler Δs = ±1 cm bei s = 20 cm: |
| ♦ | Relativer Fehler Δs = ±1 cm bei s = 20 m: 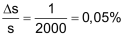 |
| Allgemein ist die Angabe des relativen Fehlers sinnvoller als die Angabe des absoluten Fehlers | |
Reste
|
Wenn man im Bereich der natürlichen Zahlen eine Zahl durch eine andere Zahl teilt, dann geht die Rechnung meistens «nicht auf», d.h. es bleibt ein ganzzahliger Rest. |
||
|
Beim Teilen einer natürlichen Zahl durch 7 zum Beispiel sind folgende Reste («7er-Reste») möglich: 1, 2, 3, 4, 5, 6 (Rechnung geht nicht auf) und 0 (Rechnung geht auf). |
||
|
Beispiel: |
||
|
55 hat den 7er-Rest 6 80 hat den 7er-Rest 3 |
||
|
a)
b) |
Multiplikation der beiden Zahlen: 55 · 80 = 4'400 →4'400 hat den 7er-Rest 4 Multiplikation der 7er-Reste beider Zahlen: 6 · 3 = 18 → 18 hat den 7er-Rest 4 |
|
| Siehe Teilbarkeit | ||
Rhomboid
| Siehe Parallelogramm |
Rhombus
|
|
|
|
Der Rhombus (die «Raute») ist ein Parallelogramm mit vier gleich langen Seiten. |
|
|
|
Für einen Rhombus gilt: |
Risse
|
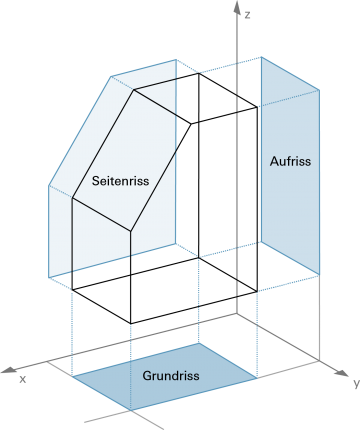
Ein Körper wird auf drei Ebenen abgebildet (projiziert), die paarweise senkrecht aufeinander stehen. Diese Abbildungen heissen «Risse». |
|
Grundriss |
«von oben gesehen» |
| Für jeden Riss gilt: Die Projektionsstrahlen sind parallel und fallen senkrecht auf die Riss-Ebene. |
| Bemerkung In der Arbeitswelt wird oft die Seitenansicht eines Objekts mit Blick in die positive y-Richtung dargestellt. |
| siehe auch Projektionen und Schrägbild |
römische Zahlen
|
Im antiken Rom wurden die natürlichen Zahlen mit Buchstaben notiert. |
|
|
Für die Notation der römischen Zahlen gibt es einige Regeln, die aber nicht immer und überall strikt eingehalten wurden: |
|
|
♦ |
Zeichen mit hohem Wert stehen links, solche mit niedrigerem Wert rechts (wie in unserer Zahlnotation). |
|
Römische Zahlen |
Zehnersystem |
|
—————————————————— |
|
| MMCMLXI | 2961 |
| Weil bei den römischen Zahlen kein Positionssystem vorliegt, ist das Rechnen mit diesen Zahlen sehr schwierig. |
runden
|
Beim Rechnen entstehen oft Zahlen mit zu vielen Ziffern. Dann wird sinnvollerweise auf- oder abgerundet. |
| 27,6351 | auf Zehner gerundet | → | 30 |
| auf Einer gerundet | → | 28 | |
| auf Zehntel gerundet | → | 27,6 | |
| auf Hundertstel gerundet | → | 27,64 | |
| auf Tausendstel gerundet | → | 27,635 |
| Ist – von den wegfallenden Stellen – die am weitesten links liegende Ziffer … | |
| • | kleiner als 5, wird sie einfach abgeschnitten («abrunden»). |
| • | grösser oder gleich 5, wird die letzte bleibende Ziffer um 1 erhöht («aufrunden»). |
| Siehe auch Überschlag | |