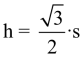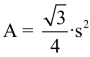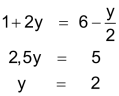Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
ganze Zahlen
Geburtenüberschuss
| Als «Geburtenüberschuss» bezeichnet man die Differenz zwischen der Geburten- und Sterbezahl innerhalb eines Jahres. | |
| Unter der «Geburtenüberschussrate» versteht man den Geburtenüberschuss bezogen auf die Einwohnerzahl. | |
| Beispiel | |
| Geburten 80'000 Sterbefälle 70'000 Bevölkerung 8,2 Mio |
|
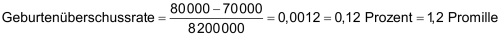 |
|
| Oft bezieht man die Geburtenüberschussrate auf 1'000 Einwohner und spricht dann von einer «Geburtenüberschussrate von 1,2». |
Geburtenüberschussrate
| siehe Geburtenüberschuss |
geometrisches Mittel
|
Das geometrische Mittel zweier positiver Zahlen ist definiert als Wurzel aus ihrem Produkt. |
|
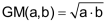 |
|
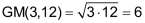 |
|
|
Geometrisch lässt sich das geometrische Mittel deuten als Seitenlänge jenes Quadrats, das den gleichen Flächeninhalt aufweist wie das Rechteck mit den Seitenlängen a und b. |
|
|
Konstruktiv findet man das geometrische Mittel mit dem Höhensatz. |
|
| siehe auch Mittelwerte | |
Geradengleichung
|
Jede mathematisch lineare Gleichung zwischen x und y wird im Koordinatensystem als Gerade dargestellt. Die «Geradengleichung» lässt sich – ausser im Fall einer Parallelen zur y-Achse – immer wie folgt schreiben: |
|
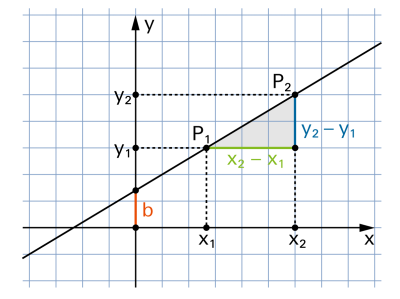 |
|
|
|
|
| a > 0 a < 0 a = 0 |
Die Gerade steigt mit wachsendem x. |
|
b ist der y-Achsenabschnitt. |
|
|
Jede lineare Gleichung der Form A ∙ x + B ∙ y + C = 0 beschreibt ebenfalls eine Gerade im Koordinatensystem. |
|
| Beispiele | |
| ♦ ♦ |
Die Gleichung y = 3 (beziehungsweise y – 3 = 0 ) beschreibt eine Parallele zur x-Achse im Abstand 3. Die Gleichung x + 2 = 0 beschreibt eine Parallele zur y-Achse links von dieser im Abstand 2. |
Geradenspiegelung
|
Siehe Achsenspiegelung |
Geschwindigkeit
|
Unter der (mittleren) Geschwindigkeit versteht man das Verhältnis zwischen dem zurückgelegtem Weg und der dazu benötigten Zeit: |
 |
| Man spricht hier auch von «Durchschnittsgeschwindigkeit». |
|
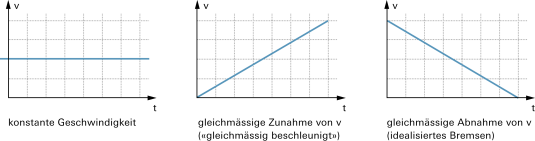
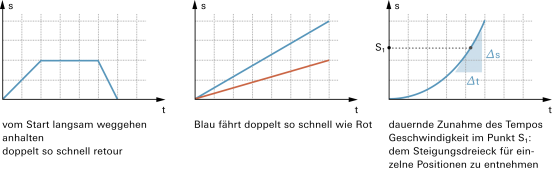
In vielen Fällen ändert sich das Tempo fortwährend. Die Geschwindigkeitsentwicklung lässt sich dann anhand von Diagrammen gut veranschaulichen: |
 |
|
Im Weg-Zeit-Diagramm erscheint die (Momentan-)Geschwindigkeit als Steigung: |
 |
ggT
|
Die Abkürzung ggT steht für «grösster gemeinsamer Teiler» von zwei oder von mehreren Zahlen. |
|
Beispiel |
|
Für das Auffinden des ggT ist der euklidsche Algorithmus ein effizienter Weg, der auch leicht über eine Tabellenkalkulation zugänglich ist. |
gleichnamig
| Siehe Bruchoperationen |
gleichseitiges Dreieck
|
Beim gleichseitigen Dreieck sind alle Winkel gleich gross (60°). |
 |
| Da die Grösse eines gleichseitigen Dreiecks durch die Seitenlänge schon eindeutig bestimmt wird, lassen sich die Höhe h und der Flächeninhalt A aus der Seitenlänge allein berechnen: |
|
|
Gleichsetzungsverfahren
| Verfahren zur algebraischen Lösung eines linearen Gleichungssystemes. | |
| Gegeben seien zwei Gleichungen: | 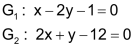 |
| Schritt 1 Beide Gleichungen auf x lösen. |
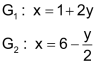 |
| Schritt 2 Beide Gleichungen gleichsetzen und auf y lösen. |
|
| Schritt 3 Das Ergebnis in Gleichung G1 einsetzen und die Gleichung auf x lösen. |
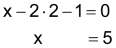 |
|
siehe auch Additionsverfahren und Einsetzungsverfahren |
|
Gleichung
|
Eine Gleichung besteht aus zwei Termen mit einer oder mehreren Variablen, die durch ein Gleichheitszeichen verbunden sind. |
||||||||
|
Eine «Gleichung lösen» heisst: |
||||||||
|
gleichwertig
| Terme, die beim Einsatz derselben Zahl für die Variable den gleichen Wert liefern, heissen gleichwertig oder äquivalent. |
| Siehe Äquivalenzumformung |
Grafik
|
Grafik ist Sammelbegriff für eine bildliche, oft geometrische Darstellung. |
|
Spezielle Beispiele: |
|
Siehe auch Graph |
Graph [ zurück ]
|
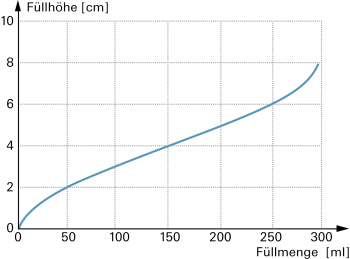
Wird der Zusammenhang zweier Grössen in einem Koordinatensystem dargestellt, spricht man von einen «Graphen». |
|
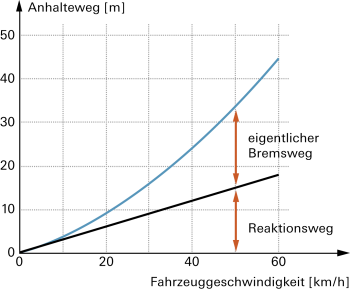
Beispiele: Füllgraphen, Weg-Zeitdiagramm, Anhalteweg eines Autos … |
 |
|
Wenn in einem Koordinatensystem der Zusammenhang zwischen zwei Grössen dargestellt ist, spricht man oft auch von «grafischer Darstellung», statt von «Graphen». |
|
 |
griechisches Alphabet
| In der Mathematik braucht man für Bezeichnungen oft auch griechische Buchstaben. Üblicherweise werden zum Beispiel Winkel mit griechischen Kleinbuchstaben bezeichnet. |
α |
Alpha |
ν |
Nü |
β |
Beta |
ξ |
Xi |
γ |
Gamma |
ο |
Omikron |
δ |
Delta |
π |
Pi |
ε |
Epsilon |
ρ |
Rho |
ζ |
Zeta |
σ |
Sigma |
η |
Eta |
τ |
Tau |
ϑ |
Theta |
υ |
Ypsilon |
ι |
Iota |
φ |
Phi |
κ |
Kappa |
χ |
Chi |
λ |
Lambda |
ψ |
Psi |
μ |
Mü |
ω |
Omega |
Grössen
|
Unter «Grössen» versteht man eine Verbindung von Zahl und Einheit. Oft spricht man präziser von «Masszahl» und «Masseinheit». |
|
|
Beispiele: |
|
|
17,5 m 4,9 l 18 cm3 |
|
|
Bei 10 m/s oder 2.50 Fr./kg oder 2,7 kg/dm3 spricht man von «zusammengesetzten Grössen». |
|
Grundmenge
|
Eine in der Statistik gebräuchliche Bezeichnung für einen untersuchten Bereich (Frauen, Männer, Jugendliche, Stimmberechtigte, Glühlampen, Laubbäume, …). |
|
Verlässliche Informationen über eine Grundmenge versucht man durch die Wahl einer geeigneten Stichprobe zu gewinnen. |
Grundoperationen
|
Als «Grundoperationen» bezeichnet man meist die Addition und die Subtraktion (beides Operationen erster Stufe) sowie die Multiplikation und die Division (Operationen zweiter Stufe). |
|
Das Wurzelziehen und Potenzieren gelten als Operationen dritter Stufe und zählen nicht zu den Grundoperationen. |
|
siehe Rechengesetze, Wurzel |
gültige Ziffern
| Messresultate ohne ausdrückliche Angabe des absoluten Fehlers sind immer so zu verstehen, dass die letzte Stelle gerundet ist: | |
|
♦ |
Die Angabe 17,4 m ist als «auf 3 gültige Ziffern genau» aufzufassen (± 0,05 m). |
| Bei Angabe von Messresultaten haben also auch Nullen am Schluss eine Bedeutung! | |